Jakie masz pytanie?

lub
lub Zadaj pytanie

Umiesz rozwiązać nierówność?

Załącznik:
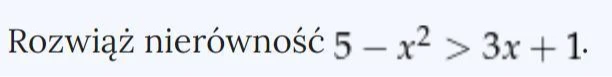
image
avatar

Gość (178.42.*.*)

  • 4 miesiące temu

Tekst z obrazu: "Rozwiąż nierówność 5 - x^2 > 3x + 1."

Rozwiążmy nierówność:

  1. Przenieś wszystkie wyrazy na jedną stronę nierówności:
    ~| 5 - x^2 - 3x - 1 > 0 ~#|

  2. Uporządkuj wyrazy:
    ~| -x^2 - 3x + 4 > 0 ~#|

  3. Pomnóż obie strony nierówności przez -1 (pamiętaj o zmianie znaku nierówności):
    ~| x^2 + 3x - 4 < 0 ~#|

  4. Rozłóż trójmian na czynniki:
    ~| x^2 + 3x - 4 = (x + 4)(x - 1) ~#|

  5. Nierówność przybiera postać:
    ~| (x + 4)(x - 1) < 0 ~#|

  6. Rozważmy miejsca zerowe: ~$ x = -4 ~#$ i ~$ x = 1 ~#$.

  7. Zbadaj znaki wyrażeń w przedziałach wyznaczonych przez miejsca zerowe:

    • Dla ~$ x < -4 ~#$: oba wyrażenia są ujemne, więc iloczyn dodatni
    • Dla ~$ -4 < x < 1 ~#$: jedno wyrażenie dodatnie, drugie ujemne, więc iloczyn ujemny
    • Dla ~$ x > 1 ~#$: oba wyrażenia dodatnie, więc iloczyn dodatni

  8. Nierówność jest spełniona dla:
    ~| -4 < x < 1 ~#|

Ostateczne rozwiązanie nierówności to:
~| x \in (-4, 1) ~#|

Podziel się z innymi:

Inne pytania z kategorii matematyka: