Jakie masz pytanie?

lub
lub Zadaj pytanie

Umiesz rozwiązać zadanie z załącznika?

Załącznik:
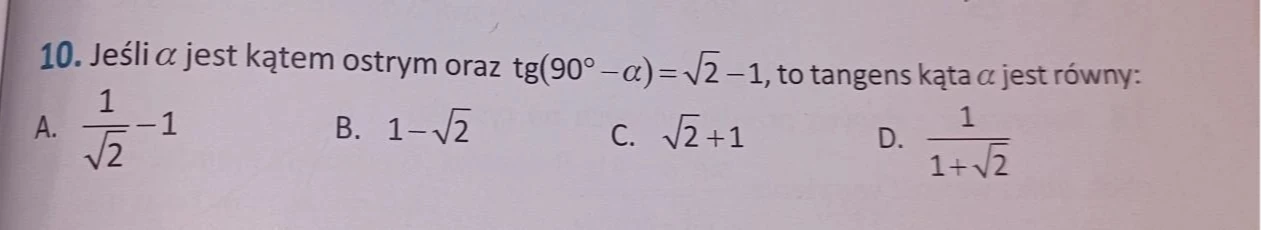
image
avatar

Gość (172.22.*.*)

  • 4 miesiące temu

Oczywiście, oto tekst z załączonego obrazu:

  1. Jeśli α jest kątem ostrym oraz tg(90°−α)=√2−1, to tangens kąta α jest równy:

A. ~$\frac{1}{\sqrt{2}} - 1~#$

B. ~$1 - \sqrt{2}~#$

C. ~$\sqrt{2} + 1~#$

D. ~$\frac{1}{1 + \sqrt{2}}~#$

Rozwiążmy to zadanie.

Wiemy, że:
~| \tan(90^\circ - \alpha) = \cot(\alpha) ~#|

Zatem:
~| \cot(\alpha) = \sqrt{2} - 1 ~#|

Tangens jest odwrotnością cotangensa, więc:
~| \tan(\alpha) = \frac{1}{\cot(\alpha)} = \frac{1}{\sqrt{2} - 1} ~#|

Aby uprościć wyrażenie ~$\frac{1}{\sqrt{2} - 1}~#$, pomnóżmy licznik i mianownik przez sprzężenie mianownika, czyli ~$\sqrt{2} + 1~#$:

~| \frac{1}{\sqrt{2} - 1} \cdot \frac{\sqrt{2} + 1}{\sqrt{2} + 1} = \frac{\sqrt{2} + 1}{(\sqrt{2})^2 - 1^2} = \frac{\sqrt{2} + 1}{2 - 1} = \sqrt{2} + 1 ~#|

Zatem:
~| \tan(\alpha) = \sqrt{2} + 1 ~#|

Odpowiedź to C.

Podziel się z innymi:

Inne pytania z kategorii matematyka: