Jakie masz pytanie?

lub
lub Zadaj pytanie

Czy trójkąt ABC jest prostokątny?

Załącznik:
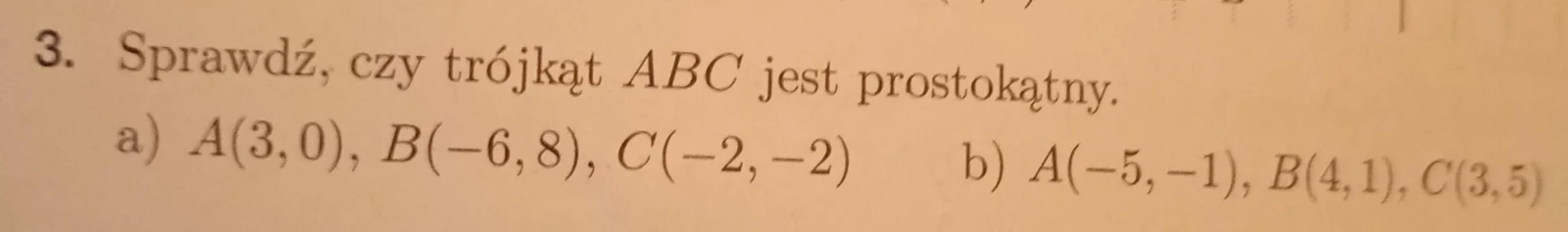
image
avatar

Gość (178.42.*.*)

  • 1 miesiąc temu

Aby sprawdzić, czy trójkąt ABC jest prostokątny, należy obliczyć długości jego boków i sprawdzić, czy spełniają twierdzenie Pitagorasa.

Dla punktów:
a) ~$ A(3, 0), B(-6, 8), C(-2, -2) ~#$

  1. Długość ~$ AB ~#$:
    ~| AB = \sqrt{(-6 - 3)^2 + (8 - 0)^2} = \sqrt{(-9)^2 + 8^2} = \sqrt{81 + 64} = \sqrt{145} ~#|

  2. Długość ~$ BC ~#$:
    ~| BC = \sqrt{(-2 + 6)^2 + (-2 - 8)^2} = \sqrt{4^2 + (-10)^2} = \sqrt{16 + 100} = \sqrt{116} ~#|

  3. Długość ~$ AC ~#$:
    ~| AC = \sqrt{(-2 - 3)^2 + (-2 - 0)^2} = \sqrt{(-5)^2 + (-2)^2} = \sqrt{25 + 4} = \sqrt{29} ~#|

Sprawdźmy twierdzenie Pitagorasa. Dla trójkąta prostokątnego jedna z kombinacji powinna spełniać:
~| AB^2 = AC^2 + BC^2 ~#|
~| \sqrt{145}^2 = \sqrt{29}^2 + \sqrt{116}^2 ~#|
~| 145 = 29 + 116 ~#|
~| 145 = 145 ~#|

Trójkąt jest prostokątny.

Dla punktów:
b) ~$ A(-5, -1), B(4, 1), C(3, 5) ~#$

  1. Długość ~$ AB ~#$:
    ~| AB = \sqrt{(4 + 5)^2 + (1 + 1)^2} = \sqrt{9^2 + 2^2} = \sqrt{81 + 4} = \sqrt{85} ~#|

  2. Długość ~$ BC ~#$:
    ~| BC = \sqrt{(3 - 4)^2 + (5 - 1)^2} = \sqrt{(-1)^2 + 4^2} = \sqrt{1 + 16} = \sqrt{17} ~#|

  3. Długość ~$ AC ~#$:
    ~| AC = \sqrt{(3 + 5)^2 + (5 + 1)^2} = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10 ~#|

Sprawdźmy twierdzenie Pitagorasa:
~| AC^2 = AB^2 + BC^2 ~#|
~| 10^2 = \sqrt{85}^2 + \sqrt{17}^2 ~#|
~| 100 = 85 + 17 ~#|
~| 100 = 102 ~#|

Trójkąt nie jest prostokątny.

Podziel się z innymi:

Inne pytania z kategorii matematyka: