Jakie masz pytanie?

lub
lub Zadaj pytanie

Czy mogę prosić o dokładniejsze informacje dotyczące zadania, które mam rozwiązać?

asymptota pozioma funkcji nowe równanie funkcji przesunięcie wykresu funkcji
Załącznik:
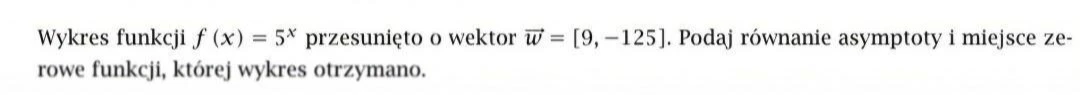
image
avatar

Gość (178.42.*.*)

  • 2 lata temu

Odpowiedź:

Treść zadania:
"Wykres funkcji ~$f(x) = 5^x~#$ przesunięto o wektor ~$\vec{w} = [9, -125]~#$. Podaj równanie asymptoty i miejsce zerowe funkcji, której wykres otrzymano."

Rozwiązanie:

  1. Przesunięcie wykresu funkcji:

    • Przesunięcie o wektor ~$\vec{w} = [9, -125]~#$ oznacza przesunięcie wykresu o 9 jednostek w prawo (wzdłuż osi x) i o 125 jednostek w dół (wzdłuż osi y).

  2. Nowa funkcja:

    • Przesunięcie wykresu funkcji ~$f(x) = 5^x~#$ o wektor ~$\vec{w} = [9, -125]~#$ daje nową funkcję ~$g(x) = 5^{(x-9)} - 125~#$.

  3. Równanie asymptoty:

    • Asymptota pozioma funkcji ~$f(x) = 5^x~#$ to ~$y = 0~#$.
    • Po przesunięciu o 125 jednostek w dół, asymptota pozioma funkcji ~$g(x) = 5^{(x-9)} - 125~#$ to ~$y = -125~#$.

  4. Miejsce zerowe:

    • Aby znaleźć miejsce zerowe funkcji ~$g(x) = 5^{(x-9)} - 125~#$, rozwiązujemy równanie ~$5^{(x-9)} - 125 = 0~#$.
    • ~$5^{(x-9)} = 125~#$.
    • ~$125~#$ to ~$5^3~#$, więc ~$5^{(x-9)} = 5^3~#$.
    • Zatem ~$x - 9 = 3~#$.
    • ~$x = 12~#$.

Podsumowanie:

  • Równanie asymptoty: ~$y = -125~#$
  • Miejsce zerowe: ~$x = 12~#$
Podziel się z innymi:

Inne pytania z kategorii matematyka: