Jakie masz pytanie?

lub
lub Zadaj pytanie

Oblicz stosując prawa działań na potęgach.

Załącznik:
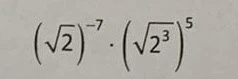
image
avatar

Gość (178.42.*.*)

  • 3 miesiące temu

Wyodrębniony tekst z obrazu:
~| \left( \sqrt{2} \right)^{-7} \cdot \left( \sqrt{2^3} \right)^5 ~#|

Aby obliczyć wyrażenie stosując prawa działań na potęgach, wykonajmy następujące kroki:

  1. Zapiszmy pierwiastki w postaci potęg:
    ~| \sqrt{2} = 2^{1/2} ~#|
    ~| \sqrt{2^3} = (2^3)^{1/2} = 2^{3/2} ~#|

  2. Podstawmy te wyrażenia do oryginalnego wyrażenia:
    ~| (2^{1/2})^{-7} \cdot (2^{3/2})^5 ~#|

  3. Zastosujmy prawo potęgowania potęgi (mnożenie wykładników):
    ~| (2^{1/2})^{-7} = 2^{(1/2) \cdot (-7)} = 2^{-7/2} ~#|
    ~| (2^{3/2})^5 = 2^{(3/2) \cdot 5} = 2^{15/2} ~#|

  4. Mamy teraz:
    ~| 2^{-7/2} \cdot 2^{15/2} ~#|

  5. Zastosujmy prawo mnożenia potęg o tej samej podstawie (dodawanie wykładników):
    ~| 2^{-7/2 + 15/2} = 2^{(15/2 - 7/2)} = 2^{8/2} = 2^4 ~#|

Ostateczny wynik to:
~| 2^4 = 16 ~#|

Podziel się z innymi:

Inne pytania z kategorii matematyka: